1948. Topological sort

You are given a directed, unweighted graph. Perform a topological sort of its vertices.

Input. The first line contains two integers: the number of vertices n (1 ≤ n ≤ 10⁵) and the number of edges m (1 ≤ m ≤ 10⁵) in the graph. The following m lines describe the edges of the graph, each given by a pair of integers – the start and end vertex numbers.

Output. If a topological sort of the graph is possible, print any valid topological ordering of the vertices as a sequence of vertex numbers. If the graph cannot be topologically sorted, print -1.

Sample input

Sample output

6 6

1 2

3 2

4 2

2 5

6 5

4 6

4 6 3 1 2 5

SOLUTION

graphs – topological sort

Algorithm analysis

The topological sorting problem can be solved using depth-first search.

· Initially, all vertices are marked white.

· When the dfs reaches a vertex, it is marked gray.

· After the processing of a vertex is complete, it is marked black.

The order of the vertices in the topological sorting corresponds to the reverse order of when they turn black. In other words, the first fully processed vertex in dfs will appear last in the topological sort, and the last processed vertex will appear first.

The vertices of the graph cannot be topologically sorted if there is a cycle in the graph. In a directed graph, this means that during dfs, there should be no edges leading to gray vertices, as such an edge indicates a cycle.

Example

The graph shown in the example has the following form:

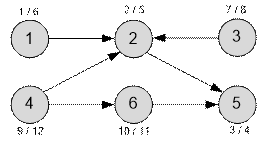
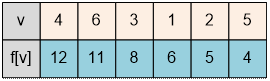
Next to each vertex v, we place labels d[v] / f[v], where d[v] is the time when the vertex starts being processed, and f[v] is the time when its processing finishes. The topologically sorted vertices are arranged in decreasing order of the values of f[v].

Algorithm implementation

Since the number of vertices in the graph is large, we’ll store the graph as an adjacency list g. To keep track of the state of the vertices, we use an array used:

· used[i] = 0, if vertex i is not visited yet (vertex is white);

· used[i] = 1, if vertex i is visited, but its processing is not yet finished (vertex is gray);

· used[i] = 2, if vertex i is processed (vertex is black);

During the execution of the depth-first search, we’ll add vertices to the top array in the order of the completion of their processing. After the algorithm finishes, the top array will contain the vertices in the reverse order of the topological sort.

vector<vector<int> > g;

vector<int> used, top;

The function dfs performs a depth-first search starting from vertex v.

void dfs(int v)

{

We enter vertex v and mark it gray.

used[v] = 1;

Iterate over all vertices to that can be reached from vertex v.

for (int to : g[v])

{

If the directed edge (v, to) leads to a gray vertex, this indicates the presence of a cycle in the graph. In this case, set flag = 1.

if (used[to] == 1) flag = 1;

If vertex to is not visited yet, recursively start a depth-first search from it.

if (used[to] == 0) dfs(to);

}

We finish processing vertex v. Mark it black and push it to the back of top array.

used[v] = 2;

top.push_back(v);

}

The main part of the program. Read the input data and construct the adjacency list of the graph.

scanf("%d %d",&n,&m);

g.resize(n+1); used.resize(n+1);

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

Perform a depth-first search on the directed graph.

flag = 0;

for(i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

If a cycle is detected during the depth-first search (flag = 1), print -1.

if (flag == 1) printf("-1");

else

Otherwise, print the vertices of the graph in the reverse order of their addition to the top array.

for(i = top.size() - 1; i >= 0; i--)

printf("%d ",top[i]);

printf("\n");

Algorithm implementation – Kahn

Store the input graph in the adjacency list g.

The in-degrees of the vertices are stored in the InDegree array.

The result of the topological sort is stored in the top array.

vector<vector<int> > g;

vector<int> InDegree, top;

deque<int> q;

Read the number of vertices n and the number of edges m.

scanf("%d %d",&n,&m);

g.resize(n+1);

InDegree.resize(n+1);

Read m edges of the graph.

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

For each edge (a, b), we increment InDegree[b] by 1.

InDegree[b]++;

}

All vertices with zero in-degree are added to the queue q.

for(i = 1; i < InDegree.size(); i++)

if (!InDegree[i]) q.push_back(i);

Continue the algorithm until the queue q is empty.

while(!q.empty())

{

Dequeue vertex v and add it to the end of the topological order list.

v = q.front(); q.pop_front();

top.push_back(v);

Remove the edges (v, to) from the graph. For each such edge, decrement the in-degree of vertex to.

for (int to : g[v])

{

InDegree[to]--;

If the in-degree of vertex to becomes zero, add it to the queue. It will then be placed in the topological order list.

if (!InDegree[to]) q.push_back(to);

}

If not all n vertices are added to the top array, then the graph contains a cycle, and topological sorting is not possible.

if (top.size() < n)

printf("-1\n");

else

{

Otherwise, print the vertices of the graph in topological order.

for (int x : top) printf("%d ", x);

printf("\n");

}

Java implementation – depth first search

import java.util.*;

import java.io.*;

public class Main

{

static ArrayList<ArrayList<Integer>> g;

static ArrayList<Integer> top = new ArrayList<Integer>();

static int used[];

static int n, m, flag = 0;

static void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < g.get(v).size(); i++)

{

int to = g.get(v).get(i);

if (used[to] == 1) flag = 1;

if (used[to] == 0) dfs(to);

}

used[v] = 2;

top.add(v);

}

public static void main(String[] args)

{

FastScanner con = new FastScanner(System.in);

n = con.nextInt();

m = con.nextInt();

g = new ArrayList<ArrayList<Integer>>();

used = new int[n+1];

for (int i = 0; i <= n; i++)

g.add(new ArrayList<Integer>());

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g.get(a).add(b);

}

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

if (flag == 1) System.out.println("-1");

else

for(int i = top.size() - 1; i >= 0; i--)

System.out.print(top.get(i) + " ");

System.out.println();

}

class FastScanner

{

BufferedReader br;

StringTokenizer st;

public FastScanner(InputStream inputStream)

{

br = new BufferedReader(new InputStreamReader(inputStream));

st = new StringTokenizer("");

}

public String next()

{

while (!st.hasMoreTokens())

{

try

{

st = new StringTokenizer(br.readLine());

} catch (Exception e)

{

return null;

}

return st.nextToken();

}

public int nextInt()

{

return Integer.parseInt(next());

}

Java implementation – Kahn

import java.util.*;

import java.io.*;

public class Main

{

static ArrayList<ArrayList<Integer>> g;

static ArrayList<Integer> top;

static int InDegree[];

static int n, m, flag = 0;

public static void main(String[] args)

{

FastScanner con = new FastScanner(System.in);

n = con.nextInt();

m = con.nextInt();

g = new ArrayList<ArrayList<Integer>>();

InDegree = new int[n+1];

for (int i = 0; i <= n; i++)

g.add(new ArrayList<Integer>());

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g.get(a).add(b);

InDegree[b]++;

}

Queue<Integer> q = new LinkedList<Integer>();

for(int i = 1; i <= n; i++)

if (InDegree[i] == 0) q.add(i);

top = new ArrayList<Integer>();

while (!q.isEmpty())

{

int v = q.poll();

top.add(v);

for (int to : g.get(v))

{

InDegree[to]--;

if (InDegree[to] == 0) q.add(to);

}

if (top.size() < n)

System.out.println("-1");

else

{

for (int x : top) System.out.print(x + " ");

System.out.println();

}

class FastScanner

{

BufferedReader br;

StringTokenizer st;

public FastScanner(InputStream inputStream)

{

br = new BufferedReader(new InputStreamReader(inputStream));

st = new StringTokenizer("");

}

public String next()

{

while (!st.hasMoreTokens())

{

try

{

st = new StringTokenizer(br.readLine());

} catch (Exception e)

{

return null;

}

return st.nextToken();

}

public int nextInt()

{

return Integer.parseInt(next());

}

Python implementation – depth first search

Increase the recursion depth.

import sys

sys.setrecursionlimit(10000)

The function dfs performs a depth-first search starting from vertex v.

def dfs(v):

We enter vertex v and mark it gray.

used[v] = 1

Iterate over all vertices to that can be reached from vertex v.

for to in g[v]:

If the directed edge (v, to) leads to a gray vertex, this indicates the presence of a cycle in the graph. In this case, set flag = 1.

if used[to] == 1:

global flag

flag = 1

If vertex to is not visited yet, recursively start a depth-first search from it.

if used[to] == 0:

dfs(to)

We finish processing vertex v. Mark it black and push it to the back of top array.

used[v] = 2

top.append(v)

The main part of the program. Read the number of vertices n and the number of edges m.

n, m = map(int, input().split())

Store the input graph in the adjacency list g. Declare the used list.

g = [[] for _ in range(n + 1)]

used = [0] * (n + 1)

Read the list of edges and construct the adjacency list of the graph.

for _ in range(m):

a, b = map(int, input().split())

g[a].append(b)

Perform a depth-first search on the directed graph.

flag = 0

top = []

for i in range(1, n + 1):

if used[i] == 0: dfs(i)

If a cycle is detected during the depth-first search (flag = 1), print -1.

if flag == 1:

print("-1")

else:

Otherwise, print the vertices of the graph in the reverse order of their addition to the top array.

for i in range(len(top) - 1, -1, -1):

print(top[i], end=" ")

print()

Python implementation – Kahn

Declare the queue q.

from collections import deque

q = deque()

Read the number of vertices n and the number of edges m.

n, m = map(int, input().split())

Store the input graph in the adjacency list g.

The in-degrees of the vertices are stored in the InDegree list.

The result of the topological sort is stored in the top list.

g = [[] for _ in range(n + 1)]

InDegree = [0] * (n + 1)

top = []

Read m edges of the graph.

for _ in range(m):

a, b = map(int, input().split())

g[a].append(b)

For each edge (a, b), we increment InDegree[b] by 1.

InDegree[b] += 1

All vertices with zero in-degree are added to the queue q.

for i in range(1, len(InDegree)):

if not InDegree[i]: q.append(i)

Continue the algorithm until the queue q is empty.

while q:

Dequeue vertex v and add it to the end of the topological order list.

v = q.popleft()

top.append(v)

Remove the edges (v, to) from the graph. For each such edge, decrement the in-degree of vertex to.

for to in g[v]:

InDegree[to] -= 1

If the in-degree of vertex to becomes zero, add it to the queue. It will then be placed in the topological order list.

if not InDegree[to]: q.append(to)

If not all n vertices are added to the top array, then the graph contains a cycle, and topological sorting is not possible.